黄石的时空回环

黄石的时空回环

Let me fly to the 🌕️

文章目录

信息

注意，本文主要是来源 1 第二章的中文翻译。

在数据挖掘领域，频繁模式挖掘（Frequent pattern mining）在算法发展过程中是最被广泛深入研究的问题之一。其中诞生了非常多的算法，最常见的是基于支持度（Support）的方法，即找到出现频率大于阈值的项目集（Itemset）。但是这些项目集不能很好刻画用户对于某个项目的兴趣，因此还有基于兴趣的方法。这里只介绍基于支持度的方法。

基本概念

频繁模式挖掘的问题根据可以描述为1

给定一个数据库 D，其中有 T1 ...TN 的交易记录
找出所有至少出现了占比超过 s 的模式 P

即找到数据集中至少出现一定次数或比例（叫做支持度）的模式。这个问题最初是起源于超市购物中经常组合购买的商品。

频繁模式挖掘也被称作是关联规则挖掘2。不过关联规则是定义在频繁模式之上的。规则 $U \Rightarrow V$ 可以被称作是支持度 s 和可信度 c 的关联规则，必须满足以下条件：

  1. $U \cup V$ 是频繁模式
  2. $U \cup V$ 的支持度除以 $U$ 的支持度大于等于 c

通俗来说，就是频繁模式中，这个规则有一定的发生的可能性。因为第一步寻找频繁模式通常是比较有挑战性的，因此主要的研究领域都集中在这里。

另外相关问题有时序模式的挖掘。比如购买商品会有一个时间戳，与购买习惯有关。

一些频繁模式挖掘的应用如下：

  • 客户交易分析（调整策略、推荐商品）
  • 网页数据挖掘
  • 软件 Bug 分析
  • 化学和生物分析

频繁模式挖掘的研究主要有四个方面：

  • 更高效的算法
  • 算法的可扩展性
  • 更复杂的数据类型
  • 应用研究

FPM 算法

传统的 FPM 是基于支持度的，算法的原型可以描述成

提示

FPM 算法原型
输入：数据库 D，最小支持度 s
输出：FP
初始化频繁模式集合 FP={}
在 FP 中插入长度为 1 的频繁模式
重复
->从 FP 中生成一个候选模式 P
->if P 在 D 中的支持度 >= s
—>把 P 加入 FP
直到 FP 中所有频繁模式都被遍历

可以看到 FPM 算法的搜索空间是非常大的，和数据集的大小成指数关系。

几乎所有的 FPM 算法都可以看作这个原型算法复杂的变种。一些最早的算法是基于连接的，比如原始的 Apriori 算法，它其实也可以看作是对枚举树的一种广度优先遍历。之后的一些算法是基于树的枚举，认为候选模式组成了词典树，并通过广度优先或者深度优先来遍历，如 TreeProjection 算法。枚举树是定义在频繁集的前缀上的，再之后的一些算法如 FP-growth 是基于后缀递归探索搜索空间的。

定义

  1. 数据集 T : $T = {T_1,T_2,\cdots,T_n}$，其中 $T_i = {x_1,x_2,\cdots,x_l}$，即数据集中有若干交易记录，每笔记录是物品的集合。
  2. 物品集 P : $P \subseteq T_i$，物品集的大小定义为包含的物品的数量。
  3. P 的支持度 : 包括 P 的交易的数量。
  4. 频繁集 : 若 P 的支持度不小于设定的标准，则 P 是频繁的。

Join-Based 算法

Join-Based 的算法通过连接的方式从频繁的 k-patterns 来产生 k+1 的候选。

Apriori

基本的想法是频繁模式的任一子集都是频繁的。那么可以通过连接的方式从长度为 k 的频繁模式中产生长度为 k+1 的频繁模式候选。

Join 连接有 k-1 个元素相同的长度为 k 的频繁模式对。

举例来说，如果 ${i_1,i_2,i_3}$ 和 ${i_1,i_2,i_4}$ 都是频繁的，那么 ${i_1,i_2,i_3,i_4}$ 也可能是频繁的。因此就可以生成一个候选模式。

为了防止生成候选的重复，规定只连接前 k-1 个元素相同的集合。

同时，值得注意的是部分候选项是可以直接被排除的，根据前面的基本想法，比如 ${i_1,i_3,i_4}$ 不是频繁的，那么之前所得到的候选可以直接被排除，不用进一步的验证。

那么整个算法的过程可以描述成

提示

Apriori 算法
输入：数据库 $T$，支持度 $s$
输出：所有 $F_i$ 的合集
用特殊的方法产生长度 1 和 2 的频繁集 $F_1,F_2$
$k:=2$
当 $F_k$ 非空时
->通过连接从 $F_k$ 中产生 $k+1$ 的候选集 $C_{k+1}$
->通过子集验证的方法排除一些候选模式
->计算候选集中的支持度来产生 $F_{k+1}$
->$k:=k+i$

在算法循环中，计算开销最大的是计算候选集中的支持度。因此有很多优化的方法和数据结构（比如哈希树）来加速这个过程。

Apriori 优化
  1. AprioriTid: 在第 k 步的时候把每个记录替换成短或空的记录，从而使得子集支持度的计算更高效。但是有时会因为多个候选是记录的子集导致的额外计算开销。
  2. AprioriHybrid: 初始迭代的时候不使用 AprioriTid。
DHP 算法3

两个优化方向：

  1. 每次迭代的时候修剪候选集。在前一轮计算的时候会保留每个集合的支持度，直接淘汰掉子集支持度不满足要求的候选集。
  2. 清理记录使得支持度计算更高效。如果某个项目在 k 的频繁集里面没有出现，那么在 k+1 的频繁集里也不会出现。那这个元素对于后面的支持度计算没有帮助，可以清理掉。

其他技巧

  1. 2 元素集合技术的特殊技巧
  2. 排除一定满足支持度要求的集合
  3. 同时计算多个频繁模式的支持度

Tree-Based 算法

Tree-Based 的算法是以集合枚举的概念出发的，候选项可以从词典树中遍历。频繁集的生成等同于建立词典树。而这类树的生长可以是广度优先也可以是深度优先的。

每一个结点代表一个物品集，根结点为 null；$I={i_1,\cdots,i_k}$ 的父节点是 ${i_1,\cdots,i_{k-1}}$。

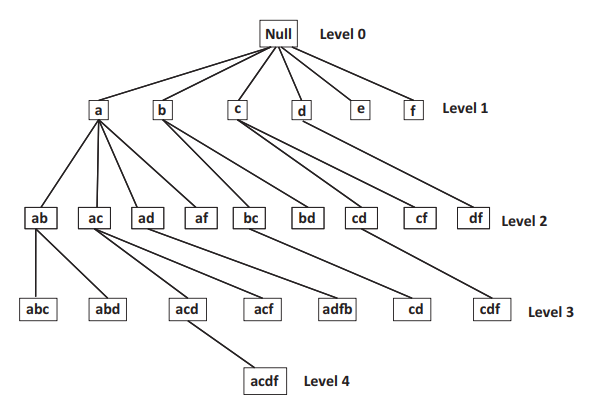
值得注意的是 Apriori 也可以被认作是词典树的方法，它使用的是广度优先的策略。

AIS

原始的词典树算法，没有用到特殊的优化方法。参考 Trie 树。

TreeProjection

TreeProjection 可以说是构建词典树的基本框架，有广度优先和深度优先两种。深度优先的方法有更高效的内存管理。

下面是一个典型的深度优先的 TreeProjection 算法。算法会不断递归扩展前缀的长度，并且只保留和前缀相关的数据。

提示

ExplorePrefix 算法
输入：数据库 $T$，最小支持度 $s$，当前前缀 $P$
计算 $T$ 中 1 元素的支持度
去除不频繁的元素
对于 $T$ 中所有的频繁 $i$
->把 $P+i$ 加入到频繁模式集中
->从 $T$ 中所有含 $i$ 的数据中构造数据库 $T_i$
->去除 $T_i$ 中词典顺序不大于 i 的所有元素
->ExplorePrefix($T_i$,$s$,$P \cup {i}$)

Vertical Mining

基本想法是通过反向列表来表示数据库，从而加快计数。

Itemtidlist
a1,2,3
b1,2,4
c1,2

算法变种：

  1. Eclat
  2. VIPER

如图找到各个长度为 1 项目的 tidlist，得到频繁项目，然后通过组合已有频繁项目得到新的集合的 tidlist，以此类推。

基于后缀的递归算法

不同于前面两类基于前缀的方法，基于后缀的算法通过后缀来扩展频繁模式。

FP-growth

具体如何构建 FPT 并通过其生成频繁参考这篇博文。

以下是从 FPT 中构建条件模式基并生成频繁项的过程。FP-growth 的方法只需要扫描两次数据库。

提示

FP-growth 算法
输入：FP-Tree $FPT$，当前后缀 $P$，最小支持度 $s$
如果 $FPT$ 是空或者单路径
->对于每条路径中结点的组合 $C$，上报所有的 $C\cup P$ 为频繁项
否则
->对于 $FPT$ 中每一个 $i$
—>$P_i={i}\cup P$
—>上报 $P_i$ 为频繁项
—>从前缀路径中移除不频繁的元素，构建 $FPT_i$
—>if $FPT_i$ 不为空
——->FP-growth($FPT_i$,$P_i$,s)

各种变种算法
  1. CT-PRO
  2. H-Mine

其他优化方法

  1. Row Enumeration
  2. Pincer-Search

参考

  1. Frequent Pattern Mining, Ed. Charu Aggarwal and Jiawei Han, Springer, 2014. ↩︎

  2. What is Frequent Pattern Mining (Association) and How Does it Support Business Analysis? ↩︎

  3. Direct Hashing and Pruning ↩︎