LLM 超参搜索指南
背景
在 LLM 预训练过程中,我们的目标是保证训练的稳定性并且效果最优。
首先,训练不稳定的情况会随着模型增大凸显。例如在 PaLM1 的训练中, 尽管使用了梯度裁剪,还是观察到了 20 次 loss 尖刺。当时研究人员采用了重启的办法回避了这个问题。不少论文猜测和优化器的超参有关,比如 Adafactor2 文中作者观察到在 Adam 中的过时的二阶动量估计(比较大的 $\beta_2$)会导致训练不稳定;Meta3 发现时域关联性会导致 Adam 不收敛。
其次,搞定了稳定性之后更重要的是训练的效果。一般来说比较小的学习率能够稳定训练,但是得到的结果是次优的。在扩展训练的规模的时候,问题会变得更加复杂,不同的模型、不同的数据都存在不同的最优超参——优化器参数(lr, $\beta_1$, $\beta_2$, lr scheduler, weight decay),参数初始化范围等等。尤其是在扩大 batch size 以期望更高效训练时,如何确定 lr 更需要经验和智慧:OpenAI4 推测 Adam 的最优学习率应该按照 $\sqrt{B}\sim B$ 之间单调递增且有上界,然而在腾讯和北大的工作 5 中发现当 batch size 扩大到一定程度,最优学习率反而出现了「涌现」现象导致应该下降。
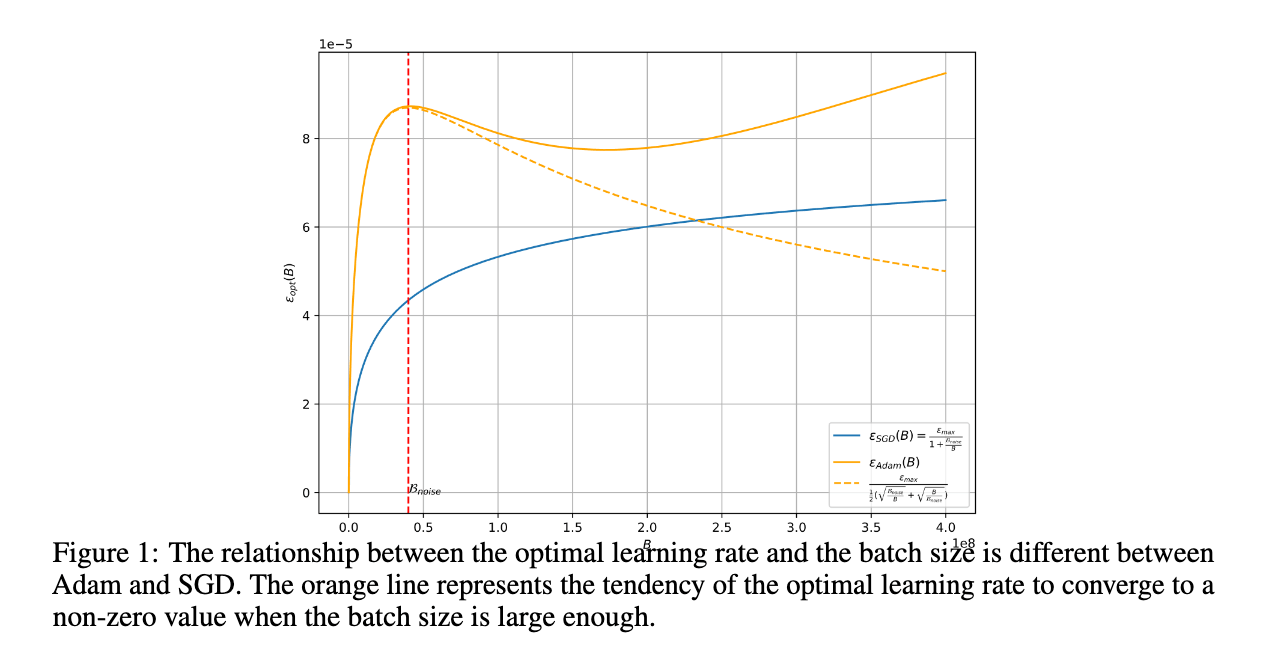
回到 LLM 预训练的背景下,上述的两种情况都是不怎么能够接受的,因为一次预训练的成本非常高昂。当然不少工作公开了训练参数,在模型、数据分布相近的情况下,直接把超参抄过来是个不错的想法。但是实际上很难做到这一点,DeepSeek6 也提到在不断清洗和优化数据过程中,模型本身 scaling 的行为是在发生变化的。
因此,一个自然而然的想法是:我们如何在每次预训练启动前,能够低成本搜索和确定最优超参?
从稳定性出发
如果我们不考虑成因比较复杂的尖刺问题,而只考虑逐渐不收敛这样的稳定性问题。根据 Deepmind 的研究 7,这种不稳定性的根因是 attention 层 logits 的增长和输出 logits 均值为负不收敛。为了解决这两个问题可以分别采用:
- QK-LayerNorm:在计算 attention logits 之前对 query 和 key 进行层归一化
- z-loss:添加辅助 $z_{loss}=10^{-4}\cdot \log^2{Z}$ 使得 $\log{Z}$ 接近 0
实验证明这些操作都可以降低模型对 lr 超参的敏感性,使得我们能够在一个较宽的范围内选择超参而没有稳定性问题。但是这和我们想要得到最优超参的目标并不一致。
在理想情况下,我们希望有这样一个小模型,能在这个模型上进行超参搜索,而这些超参和我们真正想要训练的大模型最优超参是一致的!如果从前面稳定性的角度出发,粗略一想,我们希望这个小模型和大模型在以下几个方面跟他们的尺度无关(一般来说是网络宽度):
- 前向激活的分布
- 反向梯度的分布
- 参数更新的幅度
前两者比较好理解,因为浮点数计算误差的存在,我们希望计算在当前计算的合理表示范围内;参数更新的幅度和优化器选择和学习率有关,通过控制这个幅度,可以保证在下一次迭代训练依然是稳定的。但是由于三者的相互影响,实际上只需要前向激活一直是稳定的分布即可。
当然做到上面的要求并不够,即便我们怎么调 lr,模型在稳定更新但是没有真正在做特征学习(feature learning),这样也不行。
那么有没有一种参数化方法能够做到上述的要求呢?它就是我们下面要介绍的 Maximal Update Parametrization8,即 MUP 或者 μP。
μP 和 μTransfer
μP 的设计理念来源于以下几点概念,当一个网络宽度 $n$ 取极限时,希望具有以下性质:
- 稳定性(stability):即激活 $\Theta(1)$,logits $O(1)$.
- 非平凡性(nontriviality):初始化之后 logits 的变化至少是常数,即 $\Omega(1)$.
- 特征学习(feature learning):初始化之后输出层之前的激活的变化是 $\Theta(1)$.
那么如何从这些限制条件中得到 μP,主要依赖作者前序工作 Tensor Programs——简单来说任意的神经网络计算可以程序化,从而递归得到神经网络训练任意步数下的分布。
接下来我们根据原文 9 和 Eleuther AI 的博客 10 做一个简单介绍。
首先我们回顾一下大数定律和中心极限定理:
提示
大数定律 (LLN)
如果 $x_1, \dots, x_n, \dots$ 是随机变量 $X$ 的独立同分布样本,那么
$$ \frac{1}{n} \sum_{i=1}^n x_i \to \mathbb{E}[X], \quad \mathrm{当 } n \to \infty. $$中心极限定理 (CLT)
在相同的情况下,
$$\frac{1}{\sqrt{n}} \sum_{i=1}^n \left ( x_i - \mathbb{E}[X] \right) \to \mathcal{N}(0, \sigma (X)), \quad \mathrm{当 } n \to \infty, $$其中 $\sigma (X)$ 是随机变量 $X$ 的标准差。
直觉上,我们可以认为:
当 n 很大时,$\sum_{i=1}^nx_i$ 的典型大小为
- 当 $\mathbb{E}[X]\neq0$ 时,根据 LLN 为 $\Theta(n)$
- 否则根据 CLT 为 $\Theta(\sqrt{n})$
更严格的证明请参考 Tensor Programs 系列文章。这里我们让 ChatGPT 生成一段数值实验代码,取 1000 次的结果平均,可以看到确实符合这样的规律。
信息
同样拿这个问题测试了一下 Claude Sonnet 3.5, 流程也是论文截图——翻译成中文——用数值实验验证,直接一次能够画出来,甚至不用提示加上理论线,但是 OpenAI 的图总是要更美观一点。
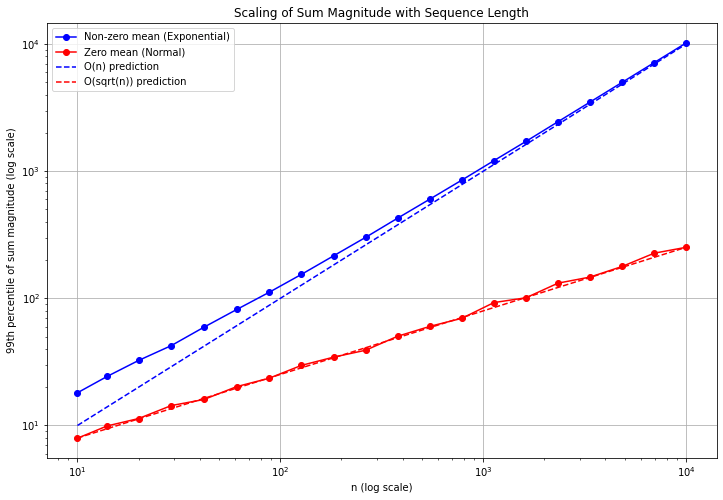 而 Google Gemini 完全没理解实验诉求。
而 Google Gemini 完全没理解实验诉求。
而在神经网络中,无论前向还是反向基本都在执行 $\mathbf{Av}$ 的计算,其中 $\mathbf{A}$ 是 $n\times n$ (或 $1\times n$ )的权重,$\mathbf{v}$ 是该层输入的激活向量。如果它们的每个元素大小是 $\Theta(1)$,那么 $\mathbf{Av}$ 每个元素($\sum_{j=1}^{n}a_{ij}v_{j}$)的大小有两种可能:
- 初始化时,按照 CLT 以 $\Theta(\sqrt{n})$ 扩展
- 训练中,因为梯度更新在原始 $\mathbf{A}$ 中引起的权重的改变以及输出层,均值非 0 时按照 LLN 以 $\Theta(n)$ 扩展
因此为了防止每层的激活不随着宽度 $n$ 的扩展而爆炸,我们需要正确设定参数的初始化范围和学习率,以抵消这两种扩展方式的影响。
以一个隐层的前向举例 10:
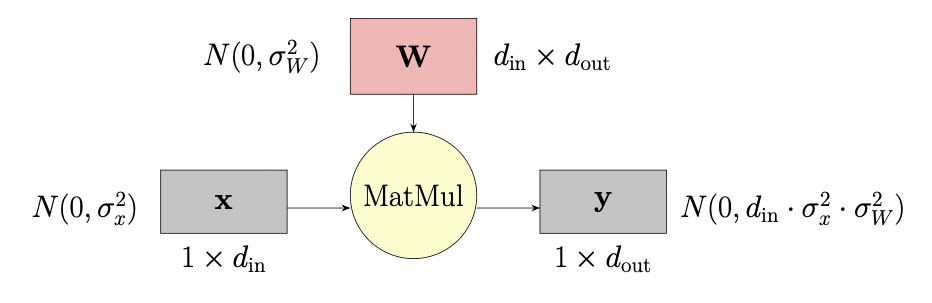
假设向量 $\mathbf{x}$ 的元素来自正态分布 $N(0, \sigma_x^2)$,并用矩阵 $\mathbf{W}$ 乘以其中的元素,矩阵 $\mathbf{W}$ 的元素来自 $N(0, \sigma_W^2)$。如果所有激活值和权重是独立的,那么结果向量 $\mathbf{y}$ 的元素将来自:$N(0, d_{\mathrm{in}} \cdot \sigma_x^2 \cdot \sigma_W^2)$(对于较大的 $d_{\mathrm{in}}$)。如果我们选择:$\sigma_W = \frac{1}{\sqrt{d_{\mathrm{in}}}}$,则:$\mathbf{y} \sim N(0, \sigma_x^2)$。这样 $\mathbf{y}$ 的尺度与层的宽度无关。
以同样的方式去分析反向传播: $\nabla_{\mathbf{x}} \mathcal{L} = (\nabla_{\mathbf{y}} \mathcal{L})(\mathbf{W})^\top$ 和权重更新对激活的影响: $\Delta \mathbf{y} = \mathbf{x} \Delta \mathbf{W}$(实际上是计算下次前向的激活的尺度)完整的初始化方差和学习率设定,使得网络能够按照前面所期望的方式训练。
我们可以得到这样一个 μP 表(版本 1),其中 fan_in/fan_out 代表权重的输入输出维度大小:
| 输入权重和所有偏置 | 输出权重 | 隐藏权重 | |
|---|---|---|---|
| 初始方差 | $1 / \mathrm{fan\_in}$ | $1 / \mathrm{fan\_in}^2$ | $1 / \mathrm{fan\_in}$ |
| SGD LR | $\mathrm{fan\_out}$ | $1 / \mathrm{fan\_in}$ | $1$ |
| Adam LR | $1$ | $1 / \mathrm{fan\_in}$ | $1 / \mathrm{fan\_in}$ |
另外注意到,对于参数矩阵 $\mathbf{W}$,初始化为 $\mathcal{N}(0,B^2)$,以 C 的学习率训练并且输出乘上一个乘子 A,对任意 $\theta > 0$,训练过程和下面是完全等价的:
- 当优化器为 SGD 时: $$ A \leftarrow A\theta, B \leftarrow B/\theta, C \leftarrow C/\theta^2 $$
- Adam 优化器当优化器为 Adam 时: $$ A \leftarrow A\theta, B \leftarrow B/\theta, C \leftarrow C/\theta $$
上面的表中令 $\theta=1/\mathrm{fan\_in}$,可得到一个更容易实现并且支持输入输出权重共享的版本 2:
| 输入权重和所有偏置 | 输出权重 | 隐藏权重 | |
|---|---|---|---|
| 初始方差 | $1/\mathrm{fan\_in}$ | $1$ | $1/\mathrm{fan\_in}$ |
| 乘子 | $1$ | $1/\mathrm{fan\_in}$ | $1$ |
| SGD 学习率 | $\mathrm{fan\_out}$ | $\mathrm{fan\_in}$ | $1$ |
| Adam 学习率 | $1$ | $1$ | $1/\mathrm{fan\_in}$ |
那么我们就可以在一个缩小宽度的小模型上模拟模拟目标模型上的行为,那么在小模型上搜索最优超参,就能够直接迁移到大模型的训练中。
μP 在 Transformers 中的实现
mup 原文提供了一个仓库实现 11,但是封装比较厉害。实际上我们只需要按照上面的表依次实现其要求即可。我们按照版本 2 依次实现初始化、前向乘子和分层学习率缩放即可。
初始化
- Embedding:注意这里不随宽度变化,因为词表大小是固定的
| |
- 隐藏层:以 MLP 层为例,
width_mult即 $m_d$,一般来说中间层也是等比例缩放(不等比也可以),对于 Attention 中的 Linear 层采用同样的缩放方式
| |
- 输出层:初始化为全 0(即和宽度无关)
前向
- Embedding:
| |
- 隐藏层:μP 中需要更改 Attention 中的 softmax scale 为 1/d,但是也有不少实现使用原版 Attention 对于超参迁移也不影响。attention_temperature 可以作为搜索超参或者直接为 1.0。在缩减的时候保持 head 维度不变,缩小 head 数量,也可以避免这个问题。
| |
- 输出层:
output_temperature可以作为搜索超参或者直接为 1.0
| |
Adam 学习率设置
既然我们的模型是固定的,我们可以把不同 name 的 layer 归类到同一组优化器参数下,按照版本 2 的方式设置缩放即可。
验证和迁移结果
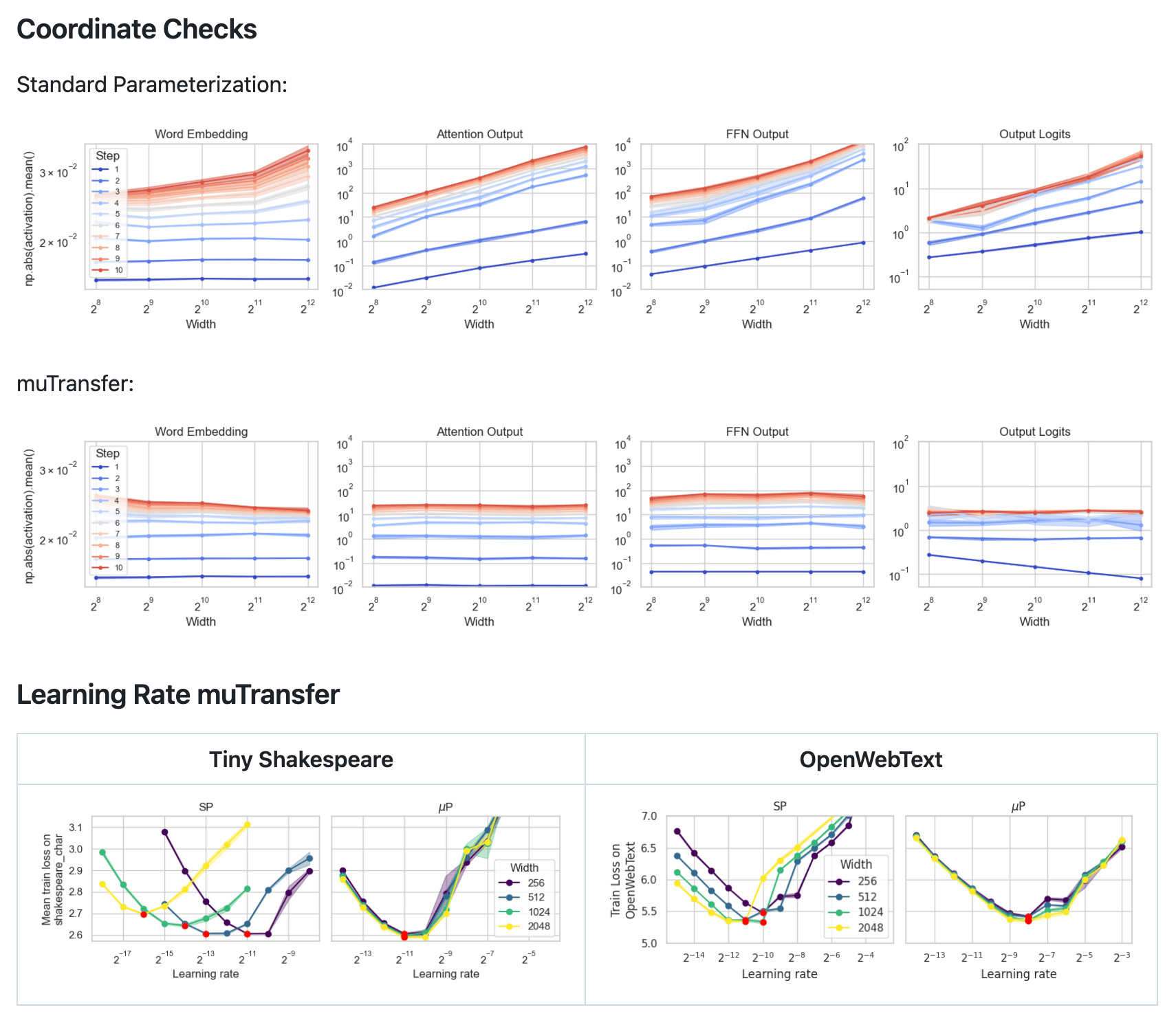
比较直观的验证实现方式正确性是检查前向激活的分布和宽度的变化,如下图所示 12,可以看到 μP 相对于标准初始化,前向对于宽度 n 是 $\Theta(1)$ 的。
并且在不同宽度模型上进行 LR 搜索,最优超参点是一致的。
谁在使用 μP
由于很少有公司开源训练代码,比较难获取模型初始化和学习率设置信息,但是我们也能从相关前向代码中看到痕迹。
比较明确使用了 μP 的模型有:
- Cerebras-GPT13,使用 40M 的代理模型搜参,迁移到 2.7B 的模型中,平稳训练的同时并且发现在 Pile 上的测试 loss 各个尺度有平均 0.43% 的提升,并且 scaling 可预测性更强。
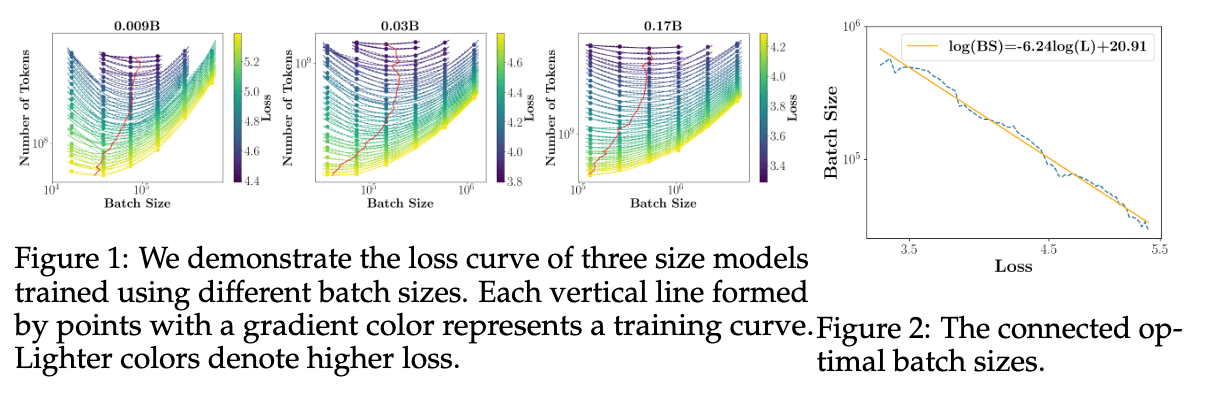
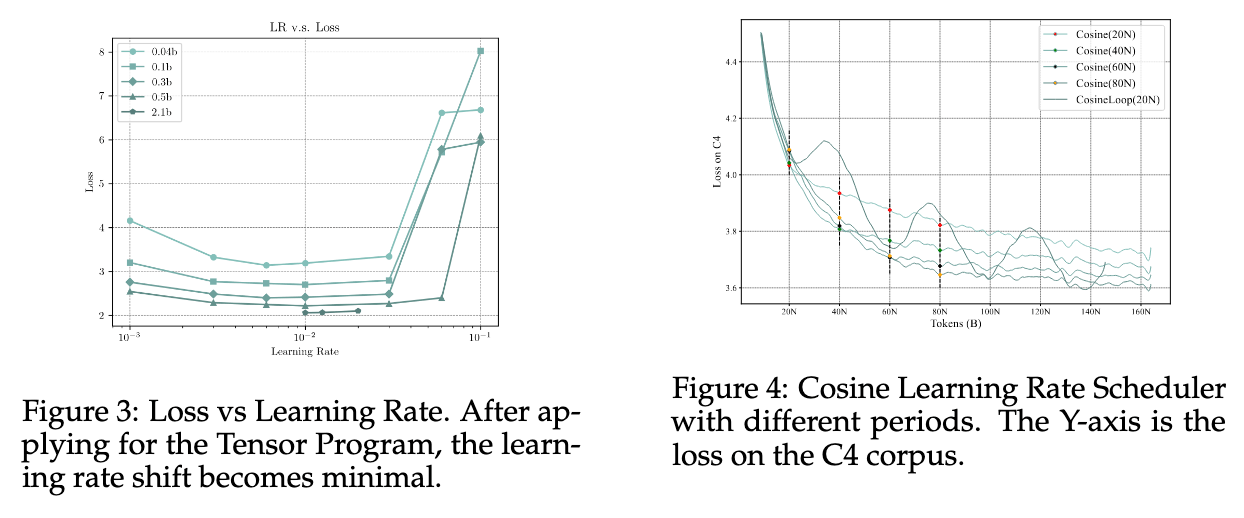
- MiniCPM 系列模型 14,均为 μP 架构,目前最大参数量为 4B,文章里比较详细介绍了通过几个小模型确定最优 BS 的 scaling 规律,再通过 μP 迁移最优超参。
- TeleChat215,最大 115B,使用大量小模型实验来验证 scaling law 规律,在不同模型结构、不同数据配比和数据清洗方式中寻找最优设计。
- Grok 系列模型 16, 总参数量 314B 的 MoE 模型,μP 作者在 x.AI,并且模型前向实现了各种乘子,并且应该严格按照原文通过 BO 搜索的超参,可以看 这段代码。
- Gemma 系列,模型前向 中有乘子出现,和 μP 的另一个版本的等效实现是一致的。另外 Deepmind 后续有更详尽的超参搜索和迁移分析文章 17。
引用
Chowdhery, A. et al. (2022) ‘PaLM: Scaling Language Modeling with Pathways’. arXiv. Available at: https://doi.org/10.48550/arXiv.2204.02311. ↩︎
Shazeer, N. and Stern, M. (2018) ‘Adafactor: Adaptive Learning Rates with Sublinear Memory Cost’. arXiv. Available at: http://arxiv.org/abs/1804.04235 (Accessed: 25 June 2023). ↩︎
Molybog, I. et al. (2023) ‘A Theory on Adam Instability in Large-Scale Machine Learning’. arXiv. Available at: http://arxiv.org/abs/2304.09871 (Accessed: 31 October 2023). ↩︎
McCandlish, S. et al. (2018) ‘An Empirical Model of Large-Batch Training’. arXiv. Available at: https://doi.org/10.48550/arXiv.1812.06162. ↩︎
Li, S. et al. (2024) ‘Surge Phenomenon in Optimal Learning Rate and Batch Size Scaling’. arXiv. Available at: http://arxiv.org/abs/2405.14578 (Accessed: 7 June 2024). ↩︎
DeepSeek-AI et al. (2024) ‘DeepSeek LLM: Scaling Open-Source Language Models with Longtermism’. arXiv. Available at: https://doi.org/10.48550/arXiv.2401.02954. ↩︎
Wortsman, M. et al. (2023) ‘Small-scale proxies for large-scale Transformer training instabilities’. arXiv. Available at: https://doi.org/10.48550/arXiv.2309.14322. ↩︎
Yang, G. and Hu, E.J. (2022) ‘Feature Learning in Infinite-Width Neural Networks’. arXiv. Available at: https://doi.org/10.48550/arXiv.2011.14522. ↩︎
Yang, G. et al. (2022) ‘Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer’. arXiv. Available at: https://doi.org/10.48550/arXiv.2203.03466. ↩︎
The Practitioner’s Guide to the Maximal Update Parameterization | EleutherAI Blog ↩︎ ↩︎
GitHub - microsoft/mup: maximal update parametrization (µP) ↩︎
GitHub - EleutherAI/nanoGPT-mup: The simplest, fastest repository for training/finetuning medium-sized GPTs. ↩︎
Dey, N. et al. (2023) ‘Cerebras-GPT: Open Compute-Optimal Language Models Trained on the Cerebras Wafer-Scale Cluster’. arXiv. Available at: https://doi.org/10.48550/arXiv.2304.03208. ↩︎
Hu, S. et al. (2024) ‘MiniCPM: Unveiling the Potential of Small Language Models with Scalable Training Strategies’. arXiv. Available at: https://doi.org/10.48550/arXiv.2404.06395. ↩︎
GitHub - Tele-AI/TeleChat2: 星辰语义大模型TeleChat2是由中国电信人工智能研究院研发训练的大语言模型,是首个完全国产算力训练并开源的千亿参数模型 ↩︎
Everett, K. et al. (2024) ‘Scaling Exponents Across Parameterizations and Optimizers’. arXiv. Available at: http://arxiv.org/abs/2407.05872 (Accessed: 1 August 2024). ↩︎